In the natural world, cooperation is everywhere. You can see it among people, of course, but not everybody cooperates all the time. Some people, as I'm sure you've heard or experienced, don't really care for cooperation. Indeed, if cooperation were something that everybody does all the time, we wouldn't even talk about it: we'd take it for granted.
But we cannot take it for granted, and the main reason for this has to do with evolution. Grant me, for a moment, that cooperation is an inherited behavioral trait. This is not a novelty mind you: plenty of behavioral traits are inherited. You may not be completely aware that you yourself have such traits, but you sure do recognize them in animals, in particular courtship displays and all the complex rituals associated with them. So if a behavioral trait is inherited, it is very likely selected for because it enhances the organisms's fitness. But the moment you think about how cooperation as a trait may have evolved, you hit a snag. A problem, a dilemma.
If cooperation is a decision that promotes increased fitness if two (or more) individuals engage in it, it must be just as possible to not engage in it. (Remember, cooperation is only worth talking about if it is voluntary.) The problem arises when in a group of cooperators an individual decides not to cooperate. It becomes a problem because that individual still gets the benefit of all the other individuals cooperating with them, but without actually paying the cost of cooperation. Obtaining a benefit without paying the cost means you get mo' money, and thus higher fitness. This is a problem because if this non-cooperation decision is an inherited trait just as cooperation is, well then the defector's kids (a defector is a non-cooperator) will do it too, and also leave more kids. And the longer this goes on, all the cooperators will have been wiped out and replaced by, well, defectors. In the parlance of evolutionary game theory, cooperation is an unstable trait that is vulnerable to infiltration by defectors. In the language of mathematics, defection--not cooperation--is the stable equilibrium fixed point (a Nash equilibrium). In the language of you and me: "What on Earth is going on here?"
Here's what's going on. Evolution does not look ahead. Evolution does not worry that "Oh, all your non-cooperating nonsense will bite you in the tush one of these days", because evolution rewards success now, not tomorrow. By that reasoning, there should not be any cooperating going on among people, animals, or microbes for that matter. Yet, of course, cooperation is rampant among people (most), animals (most), and microbes (many). How come?
The answer to this question is not simple, because nature is not simple. There are many different reasons why the naive expectation that evolution cannot give rise to cooperation is not what we observe today, and I can't here go into analyzing all of them here. Maybe one day I'll do a multi-part series (you know I'm not above that) and go into the many different ways evolution has "found a way". In the present setting, I'm going to go all "physics" with you instead, and show you that we can actually try to understand cooperation using the physics of magnetic materials. I kid you not.
Cooperation occurs between pairs of players, or groups of players. What I'm going to show you is how you can view both of these cases in terms of interactions between tiny magnets, which are called "spins" in physics. They are the microscopic (tiny) things that macroscopic (big) magnets are made out of. In theories of ferromagnetism, the magnetism is created by the alignment of electron spins in the domains of the magnet, as in the picture below.
If the temperature were exactly zero, then in principle all these domains could align to point in the same direction, so that the magnetization of the crystal would be maximal. But when the temperature is not zero (degrees Kelvin, that is), then the magnetization is less than maximal. As the temperature is increased, the magnetization of the crystal decreases, until it abruptly vanishes at the co-called "critical temperature". It would look something like the plot below.
"That's all fine and dandy", I hear you mumble, "but what does this have to do with cooperation?" And before I have a chance to respond, you add: "And why would temperature have anything to do with how we cooperate? Do you become selfish when you get hot?"
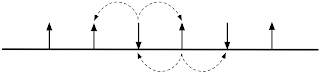
All good questions, so let me answer them one at a time. First, let us look at a simpler situation, the "one-dimensional spin chain" (compared to the two-dimensional "spin-lattice"). In physics, when we try to solve a problem, we first try to solve the simplest and easiest version of the problem, and then we check whether the solution we came up with actually applies to the more complex and messier real world. A one-dimensional chain may look like this one:
Cooperation occurs between pairs of players, or groups of players. What I'm going to show you is how you can view both of these cases in terms of interactions between tiny magnets, which are called "spins" in physics. They are the microscopic (tiny) things that macroscopic (big) magnets are made out of. In theories of ferromagnetism, the magnetism is created by the alignment of electron spins in the domains of the magnet, as in the picture below.
 |
| Fig. 1: Micrograph of the surface of a ferromagnetic material, showing the crystal "grains", which are areas of aligned spins (Source: Wikimedia). |
 |
| Fig. 2: Magnetization M of a ferromagnetic crystal as a function of temperature T (arbitrary units). |
All good questions, so let me answer them one at a time. First, let us look at a simpler situation, the "one-dimensional spin chain" (compared to the two-dimensional "spin-lattice"). In physics, when we try to solve a problem, we first try to solve the simplest and easiest version of the problem, and then we check whether the solution we came up with actually applies to the more complex and messier real world. A one-dimensional chain may look like this one:
 |
| Fig. 3: A one-dimensional spin chain with periodic boundary condition |
This chain has no beginning or end, so that we don't need to deal with, well, beginnings and ends. (We can do the same thing with a two-dimensional crystal: it then topologically becomes a torus.)
So what does this have to do with cooperation? Simply identify a spin-up with a cooperator, and a spin-down with a defector, and you get a one-dimensional group of cooperators and defectors:
C-C-C-D-D-D-D-C-C-C-D-D-D-C-D-C
So what does this have to do with cooperation? Simply identify a spin-up with a cooperator, and a spin-down with a defector, and you get a one-dimensional group of cooperators and defectors:
C-C-C-D-D-D-D-C-C-C-D-D-D-C-D-C
Now, asking what the average fraction of C's vs. D's on this string is, becomes the same thing as asking what is the magnetization of the spin chain! All we need is to write down how the players in the chain interact. In physics, spins interact with their nearest neighbors, and there are three different values for "interaction energies", depending on how the spins are oriented. For example, you could write
$$E(\uparrow,\uparrow)=a, E(\uparrow,\downarrow)=E(\downarrow,\uparrow)=b, E(\downarrow,\downarrow)=c$$.
which you could also write into matrix form like so:$$E=\begin{pmatrix} a & b\\ b& c\\ \end{pmatrix}$$
And funny enough, this is precisely how payoff matrices in evolutionary game theory are written! And because payoffs in game theory are translated into fitness, we can now see that the role of energy in physics is played by fitness in evolution. Except, as you may have noted immediately, that in physics the interactions lower the energy, while in evolution, Darwinian dynamics maximizes fitness. How can the two be reconciled?
It turns out that this is the easy part. If we replace all fitnesses by "energy=max_fitness minus fitness", then fitness maximization is turned into energy minimization. This can be achieved simply by taking a payoff matrix such as the one above, identifying the largest value in the matrix, and replacing all entries by "largest value minus entry". And in physics, a constant added (or subtracted) to all energies does not matter (remember when they told you in physics class that all energies are defined only in relation to some scale? That's what they meant by that.)
You're right, there isn't. But temperature in thermodynamics is really just a measure of how energy fluctuates (it's a bit more complicated, but let's leave it at that). And of course fitness, in evolutionary theory, is also not a constant. It can fluctuate (within any particular lineage) for a number of reasons. For example, in small populations the force that maximizes fitness (the equivalent of the energy-minimization principle) isn't very effective, and as a result the selected fitness will fluctuate (generally, decrease, via the process of genetic drift). Mutations also will lead to fitness fluctuations, so generally we can say that the rate at which fitness fluctuates due to different strengths of selection can be seen as equivalent to temperature in thermal physics.
One way to model the strength of selection in game theory is to replace the Darwinian "strategy inheritance" process (a successful strategy giving rise to successful "children-strategies") with a "strategy adoption" model, where a strategy can adopt the strategy of a competing individual with a certain probability. Temperature in such a model would simply quantify how likely it is that an individual will adopt an inferior strategy. And it turns out that "strategy adoption" and "strategy inheritance" give rise to very similar dynamics, so we can use strategy adoption to model evolution. And low and behold, the way the boundaries between groups of aligned spins change in magnetic crystals is precisely by the "spin adoption" model, also known as Glauber dynamics. This will become important later on.
OK, I realize this is all getting a bit dry. Let's just take a time-out, and look at cat pictures. After all, there is nothing that can't be improved by looking at cat pictures. Here's one of my cat eyeing our goldfish:
Needless to say, the subsequent interaction between the cat and the fish did not bode well for the future of this particular fish's lineage, but it should be said that because the fish was alone in its bowl, its fitness was zero regardless of the unfortunate future encounter.
After this interlude, before we forge ahead, let me summarize what we have learned.
1. Cooperation is difficult to understand as being a product of evolution because cooperation's benefits are delayed, and evolution rewards immediate gains (which favor defectors).
2. We can study cooperation by exploiting an interesting (and not entirely overlooked) analogy between the energy-minimization principle of physics, and the fitness-maximizing principle of evolution.
3. Cooperation in groups with spatial structure can be studied in one dimension. Evolutionary game theory between players can be viewed as the interaction of spins in a one-dimensional chain.
4. The spin chain "evolves" when spins "adopt" an alternative state (as if mutated) if the new state lowers the energy/increases the fitness, on average.
All right, let's go a-calculating! But let's start small. (This is how you begin in theoretical physics, always). Can we solve the lowly Prisoner's Dilemma?
What's the Prisoner's Dilemma, you ask? Why, it's only the most famous game in the literature of evolutionary game theory! It has a satisfyingly conspiratorial name, with an open-ended unfolding. Who are these prisoners? What's their dilemma? I wrote about this game before here, but to be self-contained I'll describe it again.
Let us imagine that a crime has been committed by a pair of hoodlums. It is a crime somewhere between petty and serious, and if caught in flagrante, the penalty is steep (but not devastating). Say, five years in the slammer. But let us imagine that the two conspires were caught fleeing the scene independently, leaving the law-enforcement professionals puzzled. "Which of the two is the perp?", they wonder. They cannot convene a grand jury because each of the alleged bandits could say that it was the other who committed the deed, creating reasonable doubt. So each of the suspects is questioned separately, and the interrogator offers each the same deal: "If you tell us it was the other guy, I'll slap you with a charge of being in the wrong place at the wrong time, and you get off with time served. But if you stay mum, we'll put the screws on you." The honorable thing is, of course, not to rat out your compadre, because they will each get a lesser sentence if the authorities cannot pin the deed on an individual. But they also must fear being had: having a noble sentiment can land you behind bars for five years with your former friend dancing in the streets. Staying silent is a "cooperating" move, ratting out is "defection", because of the temptation to defect. The rational solution in this game is indeed to defect and rat out, even though for this move each player gets a sentence that is larger than if they both cooperated. But it is the "correct" move. And herein lies the dilemma.
A typical way to describe the costs and benefits in this game is in terms of a payoff matrix:
Here, b is the benefit you get for cooperation, and c is the cost. If both players cooperate, the "row player" receives b-c, as does the "column" player. If the row player cooperates but the column player defects, the row-player pays the cost but does not reap the reward, for a net -c. If the tables are reversed, the row player gets b, but does not pay the cost at they just defected. If both defect, they each get zero. So you see that the matrix only lists the reward for the row player (but the payoff for the column player is evident from inspection).
We can now use this matrix to calculate the mean "magnetization" of a one-dimensional chain of Cs and Ds, by pretending that \({\rm C}=\uparrow\) and \({\rm D}=\downarrow\) (the opposite identification would work just as well). In thermal physics, we calculate this magnetization as a function of temperature, but I'm not going to show you in detail how to do this. You can look it up in the paper that I'm going to link to at the end. Yes I know, you are so very surprised that there is a paper attached to the blog post. Or a blog post attached to the paper. Whatever.
Let me show you what this fraction of cooperators (or magnetization of the spin crystal) looks like:
You notice immediately that the magnetization is always negative, which here means that there are always more defectors than there are cooperators. The dilemma is immediately obvious: as you increase \(r\), meaning that there is increasingly more benefit than cost), the fraction of defectors actually increases. When the net payoff increases for cooperation, you would expect that there would be more cooperation, not less. But the temptation to defect increases also, and so defection becomes more and more rational.
Of course, none of these findings are new. But it is the first time that the dilemma of cooperation was mapped to the thermodynamics of spin crystals. Can this analogy be expanded, so that the techniques of physics can actually give new results?
Let's try a game that's a tad more sophisticated: the Public Goods game. This game is very similar to the Prisoner's Dilemma, but it is played by three or more players. (When played by two players, it is the same as the Prisoner's Dilemma). The idea of this game is also simple. Each player in the group (say, for simplicity, three) can either pay into a "pot" (the Public Good), or not. Paying means cooperating, and not paying (obviously) is defection. After this, the total Public Good is multiplied by a parameter that is larger than 1 (we will call it r here also), which you can think of as a synergy effect stemming from the investment, and the result is then equally divided to all players in the group, regardless of whether they paid in or not.
Cooperation can be very lucrative: if all players in the group pay in one and the synergy factor r=2, then each gets back two (the pot has grown to six from being multiplied by two, and those six are evenly divided to all three players). This means one hundred percent ROI (return on investment). That's fantastic! Trouble is, there's a dilemma. Suppose Joe Cheapskate does not pay in. Now the pot is 2, multiplied by 2 is 4. In this case each player receives 1 and 1/3 back, which is still an ROI of 33 percent for the cooperators, not bad. But check out Joe: he paid in nothing and got 1.33 back. His ROI is infinite. If you translate earnings into offspring, who do you think will win the battle of fecundity? The cooperators will die out, and this is precisely what you observe when you run the experiment. As in the Prisoner's Dilemma, defection is the rational choice. I can show this to you by simulating the game in one dimension again. Now, a player interacts with its two nearest neighbors to the left and right:
The payoff matrix is different from that of the Prisoner's Dilemma, of course. In the simulation, we use "Glauber dynamics" to update a strategy. (Remember when I warned that this was going to be important?) The strength of selection is inversely proportional to what we would call temperature, and this is quite intuitive: if the temperature is high, then changes are so fast and random that selection is very ineffective because temperature is larger than most fitness differences. If the temperature is small, then tiny differences in fitness are clearly "visible" to evolution, and will be exploited.
The simulations show that (as opposed to the Prisoner's Dilemma) cooperation can be achieved in this game, as long as the synergy factor r is larger than the group size:
phase transition at a critical r=3, so it looks that this game also should be describable by thermodynamics.
Quick aside here. If you just said to yourself "Wait a minute, there are no phase transitions in one dimension" because you know van Hove's theorem, you should immediately stop reading this blog and skip right to the paper (link below) because you are in the wrong place: you do not need this blog. If, on the other hand, you read "van Hove" and thought "Who?", then please keep on reading. It's OK. Almost nobody knows this theorem.
Alright, I said we were going to do the physics now. I won't show you how exactly, of course. There may not be enough cat pictures on the Internet to get you to follow this. <Checks>. Actually, I take that back. YouTube alone has enough. But it would still take too long, so let's just skip right to the result.
I derive the mean fraction of cooperators as the mean magnetization of the spin chain, which I write as \(\langle J_z\rangle_\beta\). This looks odd to you because none of these symbols have been defined here. The J refers to a the spin operator in physics, and the z refers to the z-component of that operator. The spins you have seen here all point either up or down, which just means \(J_z\) is minus one or plus one here. The \(\beta\) is a common abbreviation in physics for the inverse temperature, that is, \(\beta=1/T\). And the angled brackets just mean "average". So the symbol \(\langle J_z\rangle_\beta\) is just reminding you that I'm not calculating average fraction of cooperators. I am calculating the magnetization of a spin chain at finite temperature, which is the average number of spins-up minus spins-down. And I did all this by converting the payoff matrix into a suitable Hamiltonian, which is really just an energy function.
Mathematically, the result turns out to be surprisingly simple:
$$\langle J_z\rangle=\tanh[\frac\beta2(r/3-1)] \ \ \ (1)$$
Let's plot the formula, to check how this compares to simulating game theory on a computer:
OK, let's put them side-by-side, the simulation, and the theory:
You'll notice that they are not exactly the same, but they are very close. Keep in mind that the theory assumes (essentially) an infinite population. The simulation has a finite population (1,024 players), and I show the average of 100 independent replicate simulations, that ran for 2 million updates, meaning that each of the sites of the chain was updated about 2,000 times each.
Even though they are so similar, how they were obtained could hardly be more different. The set of curves on the left was obtained by updating "actual" strings many many times, and recording the fraction of Cs and Ds on them after doing this 2 million times. (This, as any computational simulation you see in this post, was done by my collaborator on this project, Arend Hintze). To obtain the curve on the right, I just used a pencil, paper, and an eraser. It shows off the power of theory, because once you have a closed-form solution such as Eq. (1) above, not only does this solution tell you some important things, but you can now imagine using the formalism to do all the other things that are usually done in spin physics, and that we never would have thought of doing if all we did was simulate the process.
And that's exactly what Arend Hintze and I did: we looked for more analogies with magnetic materials, and whether they can teach you about the emergence of cooperation. But before I show you one of them, I will mercifully throw in some more cat pictures. This is my other cat, the younger one. She is in a box, and no, Schrödinger had nothing to do with it. Cats just like to sit in boxes. They really do.
All right, enough with the cat entertainment. Let's get back to the story. Arend and I had some evidence from a previous paper [1] that this barrier to cooperation (namely, that the synergy has to be at last as large as the group size) can be lowered if defectors can be punished (by other players) for defecting. That punishment, it turns out, is mostly meted out by other cooperators, because being a defector and a punisher at the same time turns out to be an exceedingly bad strategy. I'm honestly not making a political commentary here. Honest. OK, almost honest.
And thinking about punishment as an "incentive to align", we wondered (seeing the analogy between the battle between cooperators and defectors, and the thermodynamics of low-dimensional spin systems) whether punishment could be viewed like a magnetic field that attempts to align spins in a preferred direction.
And that turned out to be true. I will spare you again the technical part of the story (which is indeed significantly more technical), but I'll show you the side-by-side of the simulation and the theory. In those plots, I show you only one temperature \(T=0.2\), that is \(\beta=5\). But I show three different fines, meaning punishments with different strength of effect, here labelled as \(\epsilon\). The higher \(\epsilon\), the higher the "pain" of punishment on the defector (measured in terms of reduced payoff).
When we did the simulations, we also included a parameter that is the cost of punishing others. Indeed, doing so subtracts from a cooperator' net payoff: you should not be able to punish others without suffering a little bit yourself. (Again, I'm not being political here.) But we saw little effect of cost on the results, while the effect of punishment really mattered. When I derived the formula for the magnetization as a function of the cost of punishment \(\gamma\) and the effect of punishment \(\epsilon\), I found:
$$\langle J_z\rangle=\frac{1-\cosh^2(\beta\frac\epsilon4)e^{-\beta(\frac r3+\frac\epsilon2-1)}}{1+\cosh^2(\beta\frac\epsilon4)e^{-\beta(\frac r3+\frac\epsilon2-1)}} \ \ \ (2)$$
Keep in mind, I don't expect you to nod knowingly when you see that formula. What I want you to notice is that there is no \(\gamma\) there. But I can assure you, it was there during the calculation, but during the very last steps it miraculously cancelled out of the final equation, leaving a much simpler expression than the one that I had carried through from the beginning.
And that, dear reader, who has endured for so long, being propped up and carried along by cat pictures no less, is the main message I want to convey. Mathematics is a set of tools that can help you keep track of things. Maybe a smarter version of me could have realized all along that the cost of punishment \(\gamma\) will not play a role, and math would have been unnecessary. But I needed the math to tell me that (the simulations had hinted at that, but it was not conclusive).
Oh, I now realize that I never showed you the comparison between simulation and theory in the presence of punishment (aka, the magnetic field). Here it is (simulation on the left, theory on the right:
So what is our take-home message here? There are many, actually. A simple one tells you that to evolve cooperation in populations, you need some enabling mechanisms to overcome the dilemma. Yes, a synergy larger than the group size will get you cooperation, but this is achieved by eliminating the dilemma, because when the synergy is that high, not contributing actually hurts your bottom line. Here the enabling mechanism is punishment, but we need to keep in mind that punishment is only possible if you can distinguish cooperators from defectors (lest you punish indiscriminately). This ability is tantamount to the communication of one bit of information, which is the enabling factor I previously wrote about when discussing the Prisoner's Dilemma with communication. Oh and by the way, the work I just described has been published in Ref. [2]. Follow the link, or find the free version on arXiv.
A less simple message is that while computational simulations are a fantastic tool to go beyond mathematics--to go where mathematics alone cannot go [3]--new ideas can open up new directions that will open up new paths that we thought could only be pursued with the help of computers. Mathematics (and physics) thus still has some surprises to deliver to us, and Arend and I are hot on the trail of others. Stay tuned!
References
It turns out that this is the easy part. If we replace all fitnesses by "energy=max_fitness minus fitness", then fitness maximization is turned into energy minimization. This can be achieved simply by taking a payoff matrix such as the one above, identifying the largest value in the matrix, and replacing all entries by "largest value minus entry". And in physics, a constant added (or subtracted) to all energies does not matter (remember when they told you in physics class that all energies are defined only in relation to some scale? That's what they meant by that.)
"But what about the temperature part? There is no temperature in game theory, is there?"
You're right, there isn't. But temperature in thermodynamics is really just a measure of how energy fluctuates (it's a bit more complicated, but let's leave it at that). And of course fitness, in evolutionary theory, is also not a constant. It can fluctuate (within any particular lineage) for a number of reasons. For example, in small populations the force that maximizes fitness (the equivalent of the energy-minimization principle) isn't very effective, and as a result the selected fitness will fluctuate (generally, decrease, via the process of genetic drift). Mutations also will lead to fitness fluctuations, so generally we can say that the rate at which fitness fluctuates due to different strengths of selection can be seen as equivalent to temperature in thermal physics.
One way to model the strength of selection in game theory is to replace the Darwinian "strategy inheritance" process (a successful strategy giving rise to successful "children-strategies") with a "strategy adoption" model, where a strategy can adopt the strategy of a competing individual with a certain probability. Temperature in such a model would simply quantify how likely it is that an individual will adopt an inferior strategy. And it turns out that "strategy adoption" and "strategy inheritance" give rise to very similar dynamics, so we can use strategy adoption to model evolution. And low and behold, the way the boundaries between groups of aligned spins change in magnetic crystals is precisely by the "spin adoption" model, also known as Glauber dynamics. This will become important later on.
OK, I realize this is all getting a bit dry. Let's just take a time-out, and look at cat pictures. After all, there is nothing that can't be improved by looking at cat pictures. Here's one of my cat eyeing our goldfish:
 |
| Fig. 4: An interaction between a non-cooperator with an unwitting subject |
After this interlude, before we forge ahead, let me summarize what we have learned.
1. Cooperation is difficult to understand as being a product of evolution because cooperation's benefits are delayed, and evolution rewards immediate gains (which favor defectors).
2. We can study cooperation by exploiting an interesting (and not entirely overlooked) analogy between the energy-minimization principle of physics, and the fitness-maximizing principle of evolution.
3. Cooperation in groups with spatial structure can be studied in one dimension. Evolutionary game theory between players can be viewed as the interaction of spins in a one-dimensional chain.
4. The spin chain "evolves" when spins "adopt" an alternative state (as if mutated) if the new state lowers the energy/increases the fitness, on average.
All right, let's go a-calculating! But let's start small. (This is how you begin in theoretical physics, always). Can we solve the lowly Prisoner's Dilemma?
What's the Prisoner's Dilemma, you ask? Why, it's only the most famous game in the literature of evolutionary game theory! It has a satisfyingly conspiratorial name, with an open-ended unfolding. Who are these prisoners? What's their dilemma? I wrote about this game before here, but to be self-contained I'll describe it again.
Let us imagine that a crime has been committed by a pair of hoodlums. It is a crime somewhere between petty and serious, and if caught in flagrante, the penalty is steep (but not devastating). Say, five years in the slammer. But let us imagine that the two conspires were caught fleeing the scene independently, leaving the law-enforcement professionals puzzled. "Which of the two is the perp?", they wonder. They cannot convene a grand jury because each of the alleged bandits could say that it was the other who committed the deed, creating reasonable doubt. So each of the suspects is questioned separately, and the interrogator offers each the same deal: "If you tell us it was the other guy, I'll slap you with a charge of being in the wrong place at the wrong time, and you get off with time served. But if you stay mum, we'll put the screws on you." The honorable thing is, of course, not to rat out your compadre, because they will each get a lesser sentence if the authorities cannot pin the deed on an individual. But they also must fear being had: having a noble sentiment can land you behind bars for five years with your former friend dancing in the streets. Staying silent is a "cooperating" move, ratting out is "defection", because of the temptation to defect. The rational solution in this game is indeed to defect and rat out, even though for this move each player gets a sentence that is larger than if they both cooperated. But it is the "correct" move. And herein lies the dilemma.
A typical way to describe the costs and benefits in this game is in terms of a payoff matrix:
We can now use this matrix to calculate the mean "magnetization" of a one-dimensional chain of Cs and Ds, by pretending that \({\rm C}=\uparrow\) and \({\rm D}=\downarrow\) (the opposite identification would work just as well). In thermal physics, we calculate this magnetization as a function of temperature, but I'm not going to show you in detail how to do this. You can look it up in the paper that I'm going to link to at the end. Yes I know, you are so very surprised that there is a paper attached to the blog post. Or a blog post attached to the paper. Whatever.
Let me show you what this fraction of cooperators (or magnetization of the spin crystal) looks like:
 |
| Fig. 5: "Magnetization" of a 1D chain, or fraction of cooperators, as a function of the net payoff \(r=b-c\), for three different temperatures. |
Of course, none of these findings are new. But it is the first time that the dilemma of cooperation was mapped to the thermodynamics of spin crystals. Can this analogy be expanded, so that the techniques of physics can actually give new results?
Let's try a game that's a tad more sophisticated: the Public Goods game. This game is very similar to the Prisoner's Dilemma, but it is played by three or more players. (When played by two players, it is the same as the Prisoner's Dilemma). The idea of this game is also simple. Each player in the group (say, for simplicity, three) can either pay into a "pot" (the Public Good), or not. Paying means cooperating, and not paying (obviously) is defection. After this, the total Public Good is multiplied by a parameter that is larger than 1 (we will call it r here also), which you can think of as a synergy effect stemming from the investment, and the result is then equally divided to all players in the group, regardless of whether they paid in or not.
Cooperation can be very lucrative: if all players in the group pay in one and the synergy factor r=2, then each gets back two (the pot has grown to six from being multiplied by two, and those six are evenly divided to all three players). This means one hundred percent ROI (return on investment). That's fantastic! Trouble is, there's a dilemma. Suppose Joe Cheapskate does not pay in. Now the pot is 2, multiplied by 2 is 4. In this case each player receives 1 and 1/3 back, which is still an ROI of 33 percent for the cooperators, not bad. But check out Joe: he paid in nothing and got 1.33 back. His ROI is infinite. If you translate earnings into offspring, who do you think will win the battle of fecundity? The cooperators will die out, and this is precisely what you observe when you run the experiment. As in the Prisoner's Dilemma, defection is the rational choice. I can show this to you by simulating the game in one dimension again. Now, a player interacts with its two nearest neighbors to the left and right:
The payoff matrix is different from that of the Prisoner's Dilemma, of course. In the simulation, we use "Glauber dynamics" to update a strategy. (Remember when I warned that this was going to be important?) The strength of selection is inversely proportional to what we would call temperature, and this is quite intuitive: if the temperature is high, then changes are so fast and random that selection is very ineffective because temperature is larger than most fitness differences. If the temperature is small, then tiny differences in fitness are clearly "visible" to evolution, and will be exploited.
The simulations show that (as opposed to the Prisoner's Dilemma) cooperation can be achieved in this game, as long as the synergy factor r is larger than the group size:
phase transition at a critical r=3, so it looks that this game also should be describable by thermodynamics.
Quick aside here. If you just said to yourself "Wait a minute, there are no phase transitions in one dimension" because you know van Hove's theorem, you should immediately stop reading this blog and skip right to the paper (link below) because you are in the wrong place: you do not need this blog. If, on the other hand, you read "van Hove" and thought "Who?", then please keep on reading. It's OK. Almost nobody knows this theorem.
Alright, I said we were going to do the physics now. I won't show you how exactly, of course. There may not be enough cat pictures on the Internet to get you to follow this. <Checks>. Actually, I take that back. YouTube alone has enough. But it would still take too long, so let's just skip right to the result.
I derive the mean fraction of cooperators as the mean magnetization of the spin chain, which I write as \(\langle J_z\rangle_\beta\). This looks odd to you because none of these symbols have been defined here. The J refers to a the spin operator in physics, and the z refers to the z-component of that operator. The spins you have seen here all point either up or down, which just means \(J_z\) is minus one or plus one here. The \(\beta\) is a common abbreviation in physics for the inverse temperature, that is, \(\beta=1/T\). And the angled brackets just mean "average". So the symbol \(\langle J_z\rangle_\beta\) is just reminding you that I'm not calculating average fraction of cooperators. I am calculating the magnetization of a spin chain at finite temperature, which is the average number of spins-up minus spins-down. And I did all this by converting the payoff matrix into a suitable Hamiltonian, which is really just an energy function.
Mathematically, the result turns out to be surprisingly simple:
$$\langle J_z\rangle=\tanh[\frac\beta2(r/3-1)] \ \ \ (1)$$
Let's plot the formula, to check how this compares to simulating game theory on a computer:
 |
| Fig. 7: The above formula, plotted against r for the different inverse temperatures $\beta$. |
OK, let's put them side-by-side, the simulation, and the theory:
You'll notice that they are not exactly the same, but they are very close. Keep in mind that the theory assumes (essentially) an infinite population. The simulation has a finite population (1,024 players), and I show the average of 100 independent replicate simulations, that ran for 2 million updates, meaning that each of the sites of the chain was updated about 2,000 times each.
Even though they are so similar, how they were obtained could hardly be more different. The set of curves on the left was obtained by updating "actual" strings many many times, and recording the fraction of Cs and Ds on them after doing this 2 million times. (This, as any computational simulation you see in this post, was done by my collaborator on this project, Arend Hintze). To obtain the curve on the right, I just used a pencil, paper, and an eraser. It shows off the power of theory, because once you have a closed-form solution such as Eq. (1) above, not only does this solution tell you some important things, but you can now imagine using the formalism to do all the other things that are usually done in spin physics, and that we never would have thought of doing if all we did was simulate the process.
And that's exactly what Arend Hintze and I did: we looked for more analogies with magnetic materials, and whether they can teach you about the emergence of cooperation. But before I show you one of them, I will mercifully throw in some more cat pictures. This is my other cat, the younger one. She is in a box, and no, Schrödinger had nothing to do with it. Cats just like to sit in boxes. They really do.
 |
| Our cat Alex has appropriated the German Adventskalender house |
And thinking about punishment as an "incentive to align", we wondered (seeing the analogy between the battle between cooperators and defectors, and the thermodynamics of low-dimensional spin systems) whether punishment could be viewed like a magnetic field that attempts to align spins in a preferred direction.
And that turned out to be true. I will spare you again the technical part of the story (which is indeed significantly more technical), but I'll show you the side-by-side of the simulation and the theory. In those plots, I show you only one temperature \(T=0.2\), that is \(\beta=5\). But I show three different fines, meaning punishments with different strength of effect, here labelled as \(\epsilon\). The higher \(\epsilon\), the higher the "pain" of punishment on the defector (measured in terms of reduced payoff).
When we did the simulations, we also included a parameter that is the cost of punishing others. Indeed, doing so subtracts from a cooperator' net payoff: you should not be able to punish others without suffering a little bit yourself. (Again, I'm not being political here.) But we saw little effect of cost on the results, while the effect of punishment really mattered. When I derived the formula for the magnetization as a function of the cost of punishment \(\gamma\) and the effect of punishment \(\epsilon\), I found:
$$\langle J_z\rangle=\frac{1-\cosh^2(\beta\frac\epsilon4)e^{-\beta(\frac r3+\frac\epsilon2-1)}}{1+\cosh^2(\beta\frac\epsilon4)e^{-\beta(\frac r3+\frac\epsilon2-1)}} \ \ \ (2)$$
Keep in mind, I don't expect you to nod knowingly when you see that formula. What I want you to notice is that there is no \(\gamma\) there. But I can assure you, it was there during the calculation, but during the very last steps it miraculously cancelled out of the final equation, leaving a much simpler expression than the one that I had carried through from the beginning.
And that, dear reader, who has endured for so long, being propped up and carried along by cat pictures no less, is the main message I want to convey. Mathematics is a set of tools that can help you keep track of things. Maybe a smarter version of me could have realized all along that the cost of punishment \(\gamma\) will not play a role, and math would have been unnecessary. But I needed the math to tell me that (the simulations had hinted at that, but it was not conclusive).
Oh, I now realize that I never showed you the comparison between simulation and theory in the presence of punishment (aka, the magnetic field). Here it is (simulation on the left, theory on the right:
So what is our take-home message here? There are many, actually. A simple one tells you that to evolve cooperation in populations, you need some enabling mechanisms to overcome the dilemma. Yes, a synergy larger than the group size will get you cooperation, but this is achieved by eliminating the dilemma, because when the synergy is that high, not contributing actually hurts your bottom line. Here the enabling mechanism is punishment, but we need to keep in mind that punishment is only possible if you can distinguish cooperators from defectors (lest you punish indiscriminately). This ability is tantamount to the communication of one bit of information, which is the enabling factor I previously wrote about when discussing the Prisoner's Dilemma with communication. Oh and by the way, the work I just described has been published in Ref. [2]. Follow the link, or find the free version on arXiv.
A less simple message is that while computational simulations are a fantastic tool to go beyond mathematics--to go where mathematics alone cannot go [3]--new ideas can open up new directions that will open up new paths that we thought could only be pursued with the help of computers. Mathematics (and physics) thus still has some surprises to deliver to us, and Arend and I are hot on the trail of others. Stay tuned!
References
[1] A. Hintze and C. Adami, Punishment in Public Goods games leads to meta-stable phase transitions and hysteresis, Physical Biology 12 (2005) 046005.
[2] C. Adami and A. Hintze, Thermodynamics of evolutionary games. Phys. Rev. E 97 (2018) 062136
[3] C. Adami, J. Schossau, and A. Hintze, Evolutionary game theory using agent-based methods, Phys. Life Reviews. 19 (2016) 38-42.
[2] C. Adami and A. Hintze, Thermodynamics of evolutionary games. Phys. Rev. E 97 (2018) 062136
[3] C. Adami, J. Schossau, and A. Hintze, Evolutionary game theory using agent-based methods, Phys. Life Reviews. 19 (2016) 38-42.







Very nice work indeed.
ReplyDeleteOne thing though, something is a bit wrong with the code in the page, some of the equations dont load: e.g. 'derive the mean fraction of cooperators as the mean magnetization of the spin chain, which I write as $\langle J_z\rangle_\beta$'
Thank you for pointing this out. I figured out that this happens because MathJax has switched from using the $xxx$ for inline LaTeX to \(xxx\). It is now all fixed!
Delete